こんにちは、三重の家庭教師です。日に日に涼しくなってきましたね。さて、本日は楕円の面積の公式を紹介します。楕円は「だえん」と読み、卵のような形をした図形です。

楕円の面積の公式は、高校の数学Ⅲで習います。高校で習う公式なので、「難しい公式なのでは?」と思う方もいるかもしれませんが、実は意外に簡単なんですよ。
【目次】
スポンサーリンク
楕円の面積の公式
私がなぜ「楕円の面積の公式は簡単だ!」と断言するのかというと、楕円の面積の公式は、円の面積の公式と非常に似ているからです。下の図を見てください。
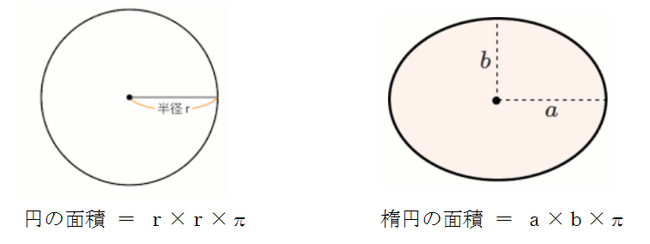
円の面積の公式は、「半径×半径×円周率」、つまり「r×r×π」でしたね。もし、円の面積の公式を知らない人は円の面積の公式!この問題をやれば円の面積は余裕だぜ!で確認してください。
一方、本題である楕円の面積の公式は、
楕円の面積 = a × b × π
です。あなたはこの公式を見て、何か気づいたことはありませんか?
楕円の面積 = a × b × π
です。あなたはこの公式を見て、何か気づいたことはありませんか?
私は初めて楕円の公式を見たとき、「楕円の半径であるaとbを、円の半径と思えば、円の面積の公式と同じじゃん!」と思いました。
円の面積の公式と同じように、楕円の面積の公式も、「半径を2回かける感じ!」と覚えておけば、小学生の子でも覚えられそうな公式だと思いませんか。
ちなみに、楕円の半径の部分にも名前があり、長い方の半径であるaの部分を長半径(長径)、bの部分を短半径(短径)と言います。「短い半径だから短半径」なんてそのままのネーミングですね!
この名前を使うと、楕円の面積の公式は
楕円の面積 = 長半径 × 短半径 × π
ということになります。それでは、楕円の面積の求め方を下の例で解説します。
スポンサーリンク
楕円の面積の求め方
例① 下図の長半径が5、短半径が3の楕円の面積を求めよう。
例① 下図の長半径が5、短半径が3の楕円の面積を求めよう。
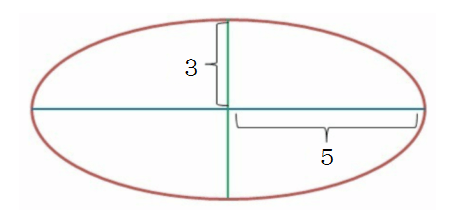
長い方の半径が5、短い方の半径が3なので、a=5、b=3なので、公式に当てはめると、
楕円の面積 = 5 × 3 × π = 15π
これぐらいのレベルなら、小学生の子でも計算できそうですね。それでは、次の問題は高校の数Ⅲレベルの問題を紹介します。
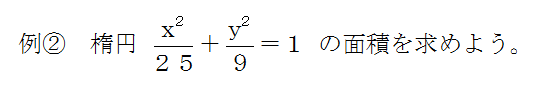
さて、今度の問題は、例1と違って長半径aと短半径bの長さがわかっていないので、自分でaとbの値を求めないといけません。ではどうすればいいか?
aとbの値を求めるには、楕円の方程式を覚えている必要があります。あなたは、楕円の方程式を覚えていますか?楕円の方程式は、
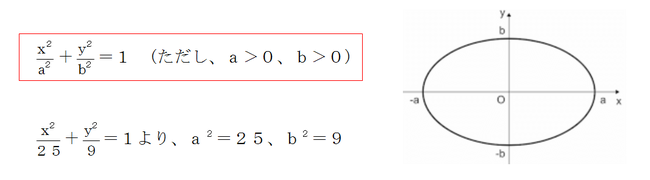
です。赤線で囲まれた楕円の方程式から、aとbの値を求めることができます。a2=25から、a=5、b2=9から、b=3となりますね。
これで長半径aが5、短半径bが3とわかったので、後は楕円の面積の公式にぶち込んで計算するだけです。よって、a=5、b=3より、
楕円の面積 = 5 × 3 × π = 15π
となります。気づいた方もいるかもしれませんが、実は例②の問題は、例①と全く同じなんです。同じ問題なのに、問題の作り方によって、全然レベルは違いますね。
それでは、最後に楕円の面積の公式を利用した問題をもう1つ紹介します。楕円の面積の公式を覚えていると、例3のような媒介変数と面積に関する問題を簡単に解くことができることがあります。
例③ 0≦θ≦2πでθを媒介変数とするx=3cosθ、y=2sinθで囲まれた面積Sを求めよう。
これで長半径aが5、短半径bが3とわかったので、後は楕円の面積の公式にぶち込んで計算するだけです。よって、a=5、b=3より、
楕円の面積 = 5 × 3 × π = 15π
となります。気づいた方もいるかもしれませんが、実は例②の問題は、例①と全く同じなんです。同じ問題なのに、問題の作り方によって、全然レベルは違いますね。
それでは、最後に楕円の面積の公式を利用した問題をもう1つ紹介します。楕円の面積の公式を覚えていると、例3のような媒介変数と面積に関する問題を簡単に解くことができることがあります。
例③ 0≦θ≦2πでθを媒介変数とするx=3cosθ、y=2sinθで囲まれた面積Sを求めよう。
上の例③のような問題は、「媒介変数と面積」に関する分野でよく出題されます。そして、この問題を学校では置換積分法を使って解くことが多いです。
しかし、実際に置換積分法で解いてもらったらわかると思いますが、計算量がけっこうエグくて大変なんです。でも、楕円の面積の公式を使うと計算量がすごく減るんですよ!
ぜひ、置換積分を使った解き方と楕円の面積の公式を利用した解き方で、その違いを体感してみてください。私はこの問題のおかげで楕円の面積の公式の便利さを知りました。
しかし、実際に置換積分法で解いてもらったらわかると思いますが、計算量がけっこうエグくて大変なんです。でも、楕円の面積の公式を使うと計算量がすごく減るんですよ!
ぜひ、置換積分を使った解き方と楕円の面積の公式を利用した解き方で、その違いを体感してみてください。私はこの問題のおかげで楕円の面積の公式の便利さを知りました。
まとめ
ということで、今回は楕円の面積の公式を紹介しました。円の面積の公式は「半径×半径×円周率」で、楕円の面積の公式は「長径×短径×円周率」と、円の面積の公式の覚え方とほぼ同じと覚えておきましょう!
スポンサーリンク


コメント